Substructure Searching with Indexes

What is Indexing?

Indexing is pre-computing the answers to portions of expected questions before they’re asked, so that when the question comes, it can be answered quickly.

Take your favorite search engine (AOL, Yahoo!, Google, MSN, …) for example. Without indexing, they might wait until you ask for “John Hartford Bluegrass”, then start searching the web, and in a year or two find all the web pages about the deceased banjo/fiddle player and steamboat captain. That would probably not impress you.

Instead, these search engines search the web before you ask your question, and build an index of the words they find. When you type in “Bluegrass John Hartford”, they already know all of the pages that have “John”, all of the pages with “Hartford”, and all of the pages with “Bluegrass”. Instead of searching, they examine their index, and find pages that are on all three lists, and quickly find your results. (NB: It’s actually a lot more complex, but this illustrates the main idea of indexing.)

Indexes for Chemicals

Instead of indexing words, cheminformatics systems index substructures. Although there are many schemes for doing this, cheminformatics systems all use the same fundamental principle: they decompose the molecule into smaller bits, and index those.

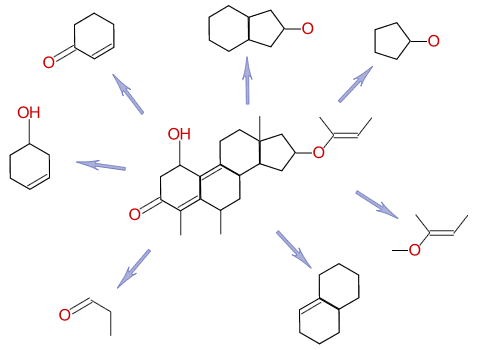
Roughly speaking, a cheminformatics system will index each of the substructures (fragments) above, so that every molecule that contains each fragment is known.

When a query is entered, the cheminformatics system breaks apart the query using the same technique, to find all of the fragments in the query. It then checks its index for each fragment, and combines the lists it finds to get only those molecules that have all of those fragments.

This doesn’t mean that all molecules returned by the index actually are matches. In the language of databases, we say the index will return false positives, candidate molecules that don’t actually match the substructure search.

Consider our example of searching for “John Hartford” - the index might return many pages that have both “John” and “Hartford”, yet have nothing to do with bluegrass music or steamboats. For example, it might return a page containing, “President John F. Kennedy visited Hartford, Connecticut today…”. To confirm that the search system has found something relevant, it must check the pages return from the index to ensure that the specific phrase “John Hartford” is present. However, notice that this is much faster than searching every page, since the overwhelming majority of web pages were instantly rejected because they have neither “John” nor “Hartford” on them.

Similarly, a chemical fragment index serves to find only the most likely molecules for our substructure match - anything that the index didn’t find is definitely not a match. But we still have to examine each of the molecules returned by the indexing system and verify that the complete substructure for which we are searching is present.

NP-Complete - A Little about Computability

Searching through a page of text for the words “John Hartford” is pretty easy for a modern computer. Although false positives returned by the index are a nuisance and impair performance, they are not a catastrophe. Not so for substructure matching. Unfortunately, substructure matching falls into a category of “hard” mathematical problems, which means false positives from the index are a big problem.

Substructure matching (finding a certain functional group within a molecule) is an example of what mathematicians call graph isomorphism, and is in a class of problems called NP Complete. Roughly speaking, this means the time it takes to do a substructure search is non-polynomial, i.e. exponential in the number of atoms and bonds. To see why this is a computational disaster, compare two tasks, one that takes polynomial time, k₁*N², versus one that takes exponential time k₂*2^N. Our polynomial task is bad enough: If we double N, it takes four times as long to solve. But the exponential task is worse: Every time we add an atom it doubles. So going from one atom to two doubles the time, and going from 100 atoms to 101 atoms doubles the time. Even if we can get k₂ down to a millionth of k₁, we’re still in trouble - a million is just 2²⁰ or twenty atoms away.

It has been mathematically proven that substructure searching is in the set of NP Complete problems, so there’s no point wasting our time searching for a polynomial algorithm. The good news is that most molecules have “low connectivity”, meaning most atoms have fewer than four bonds, unlike the weird and twisted graphs that mathematicians consider. In practice, most substructure matching can be done in polynomial time around N² or N³. But even with this improvement, substructure matching is an “expensive” time-consuming task for a computer.

The key point is that indexing is particularly important for cheminformatics systems. The typical modern computer can only examine a few thousand molecules per second, so examining millions of molecules one-by-one is out of the question. The indexing done by a modern cheminformatics system is the key to its performance.